Why we Overestimate the Odds of Finding Multibaggers in Smallcaps?

In September’s FOF, I gave a presentation on the Opportunity and Challenges in Smallcap Investing. A recurrent question post the presentation was about how Smallcaps which have become Largecaps have generated a lot of wealth and consequently doesn’t it make Smallcaps attractive? Here’s a thought many share: When we look at the list of past multibaggers, we often find that many of those stocks started as Smallcaps. This leads some to infer that the probability of a smallcap becoming a multibagger is very high.

What does the actual data tell us? Let’s define a stock that offers a 30% Compound Annual Growth Rate (CAGR) over five years as a ‘multibagger’. Analyzing past data (from 2013 to 2018) from the top 500 stocks, we find that there’s an 11% chance of any stock becoming a multibagger. Focusing only on Smallcaps, that probability rises slightly to 13%. In other words, out of 250 Smallcap stocks, only about 33 might deliver such returns. Furthermore, there’s a 16% chance of a Smallcap stock declining by 50% over five years, compared to 14% for the broader stock group. This data suggests we might be greatly overestimating the allure of Smallcaps.

But the interesting question is why do we overestimate these odds? The answer lies in a fallacy most of us fall prey to – Base Rate Fallacy. What appears to us a high probability phenomenon actually turns out to be a low probability phenomenon.

To understand Base Rates, we need to understand Bayes Theorem; a cornerstone of probability theory. And for that we need some notation. At first glance, the mathematical notation may seem daunting, but trust me, it’s quite simple and intuitive.

P(A) : Probability of event A occurring
P(A | B) : Probability of event A occuring, given that B has occurred. In other words, if we know that B is true, then what is the probability of A

Now, Bayes rule states that:

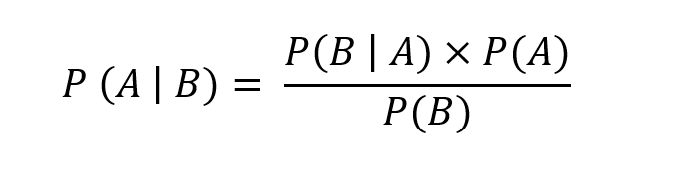
Translated to plain terms: If you want to know the probability of A happening given that B has happened – P(A|B), you can figure it out by looking at:

P(B|A) – How often B happens when A happens,
P(A) – The overall likelihood of A happening on its own, and
P(B) – Dividing those by how often B happens in general.”

A common error is to confuse P(A|B) with P(B|A). This error is also called the Inverse Probability error

Now, with this context let’s evaluate the probability of smallcaps turning to large caps.
So let’s put this in notation. We know a stock is a multibagger and we believe many of these are smallcaps. When we look at past multibaggers we find that 60% of the multibaggers were smallcaps.

P (Smallcap | Multibagger) = 0.6

It might be tempting to take this 60% as the probability that a Small Cap would become a Multbagger. But as we will see that would be a major error in estimating probabilities. When you think about it, what we really want to know is if a given stock is a smallcap, what is the probability that it will become a multibagger i.e. P (Multibagger | Smallcap)

By Bayes Theorem :

Of the top 500 stocks, half are Smallcap. So we know the probability of smallcap – P(Smallcap) = 0.5

Also, of all the listed stocks we found that approximately 11% of stocks become multibaggers; so P(Multibagger) = 0.11

Now, we have the required probabilities to calculate the probability we want

P (Multibagger | Smallcap) = (0.6 x 0.11)/0.5 = 0.13 i.e. 13%

The reason for this low probability is that the overall base rate for a stock becoming a multibagger – P(Multibagger) is extremely low (11%) and that number dominates the probability of a smallcap becoming a multibagger. Our intuition makes us focus on P(Smallcap | Multibagger) but the number that influences the end probability much more is P(Multibagger). You can try different assumptions for P(Smallcap|Multibagger) and P(Multibagger) in the formula and what you will find is that so long as P(Multibagger) is very low, the end probability will also be low.

Once you understand and appreciate inverse probabilities, you will see them everywhere. For example: many studies and books focus on very successful companies and try to identify the traits common to them. Again this is actually an Inverse Probability problem and prone to Base Rate fallacy. By starting with a list of very successful companies and then identifying a common trait, we are finding P(Trait | Success). What we are actually interested in is P(Success | Trait) i.e. if a company has a given Trait then what is the probability that it will be successful.

How can we mitigate this fallacy? When probabilistic judgements, especially for low probability events, we need to take a step back and ask ourselves whether the Probability we have calculated or assumed is what is relevant to the decision or have we estimated an Inverse probability where we need to account for base rates. By ensuring that we critically evaluate the information at hand and avoid jumping to conclusions based on intuition or selective data, we can make more informed and rational decisions.

References:

• This is a wonderful video to understand Bayes Theorem by the channel – 3Blue1Brown : https://youtu.be/HZGCoVF3YvM?si=KzIfHwyjZ32lx8HA